



: 仕事はベクトル量?
: 仕事
: 仕事をされたかチェック!
目次
仕事の正負はどのように決まっているのか考えてみましょう。
仕事が物体に加えた力と移動距離の積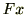 [J]だということはイメージしてもらえたと思います。ではその正負はどのように決まっているのでしょうか?ここで次のような状態を考えてください。
[J]だということはイメージしてもらえたと思います。ではその正負はどのように決まっているのでしょうか?ここで次のような状態を考えてください。
お兄ちゃんと妹が遊んだ車を片付けようとしています。お兄ちゃんが進ませようとしている方向が正しいのですが、妹がいたずらして邪魔をしています。このときお兄ちゃんと妹は車にどのような力を加えているでしょうか?
2人が車を押す力の大きさが等しいと、車はどちらにも動きません。そのときの様子は図22のようになります。
さてこのとき2人とも力は加えていますが、その力を加えている対象である車は全く動きませんから、仕事はしていないことになりますね。つまり「力を加えても物体が動かなければ仕事はしていない」わけです。
そうこうしていると、お兄ちゃんも怒ってちょっと力を入れたようです。お兄ちゃんの押している方向へ車が動き始めました。
このときお兄ちゃんが車にした仕事 はどのようになるでしょうか?もちろん今までしっかりとイメージを構築してきた皆さんなら問題ないでしょう。力
はどのようになるでしょうか?もちろん今までしっかりとイメージを構築してきた皆さんなら問題ないでしょう。力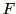 [N]で距離
[N]で距離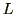 [m]移動させたわけですから、
[m]移動させたわけですから、
となります。ここで問題なのは妹が車にした仕事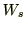 です。「えっ!?妹って車に仕事しているの?」と思っている方もいらっしゃるかも知れません。が、もちろん妹も車に仕事を加えています。
です。「えっ!?妹って車に仕事しているの?」と思っている方もいらっしゃるかも知れません。が、もちろん妹も車に仕事を加えています。
仕事の定義を思い出してください。「物体に力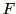 [N]を加えて距離
[N]を加えて距離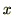 [m]だけ動かしたとき、その力
[m]だけ動かしたとき、その力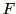 [N]は物体に仕事
[N]は物体に仕事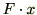 [J]を与えた」でしたね。妹は車に力
[J]を与えた」でしたね。妹は車に力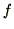 [N]を加えています。そして車が移動してしまったので、移動距離も発生しています。だったら仕事は当然生じます。
しかし、妹が加えた仕事はお兄ちゃんが加えた仕事とは少々違います。さて何が違うのでしょうか?車の移動方向と、車に加えている力の方向をよく確認してみてください。
[N]を加えています。そして車が移動してしまったので、移動距離も発生しています。だったら仕事は当然生じます。
しかし、妹が加えた仕事はお兄ちゃんが加えた仕事とは少々違います。さて何が違うのでしょうか?車の移動方向と、車に加えている力の方向をよく確認してみてください。
お兄ちゃんが加えている力の方向と車の移動方向は同じですが、妹が加えている力の方向は、車の移動方向と逆方向を向いています。つまり、お兄ちゃんは車を動かすために仕事を加えたのですが、妹は車の動きを邪魔するために仕事を加えたわけです。確認するところはただ一つ「移動方向と力を加えた向き」です。
この妹がした仕事のように、「物体の運動方向と逆方向に加えた力が物体にする仕事」を負の仕事と定義します。移動方向と力の方向が逆ですので、移動方向を正にとって
となります。つまりお兄ちゃんが車にした仕事は正の仕事
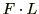 [J]で、妹が車にした仕事は邪魔する仕事
[J]で、妹が車にした仕事は邪魔する仕事
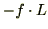 [J]ですから、トータルで車がされた仕事
[J]ですから、トータルで車がされた仕事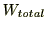 は
は
となります。この式(6)で表されている内容を別の角度から見てみましょう。
ではもう一度しっかりと図23を見てください。
車に働く力はお兄ちゃんの力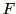 [N]と妹の逆方向の力
[N]と妹の逆方向の力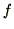 [N]があります。ですから、車に働く力の合力は当然右方向へ
[N]があります。ですから、車に働く力の合力は当然右方向へ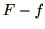 [N]となりますね。では図24にお兄ちゃんと妹が出す力の合力を示し、合成した結果、妹を取り除いた状態図を図24に示します。
[N]となりますね。では図24にお兄ちゃんと妹が出す力の合力を示し、合成した結果、妹を取り除いた状態図を図24に示します。
つまり、仕事を出す前に合力を出してしまうと、結局お兄ちゃんが2人の力の差分
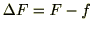 [N]で進行方向へ距離
[N]で進行方向へ距離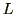 [m]だけ移動させていると考えることが出来るので、このときの仕事を
[m]だけ移動させていると考えることが出来るので、このときの仕事を
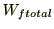 とすると
とすると
となり、結局式(6)と式(7)は同じことを言っていると分かります。
したがって、車がされた仕事を考えるときは「車に加わるそれぞれの力がした仕事の合計」と考えてもいいですし、「車に加わる力の合力がした仕事」と考えてもいいわけです。この結果から逆に、お兄ちゃんだけだったら
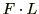 [J]の仕事が出来たはずなのに、妹が仕事をした結果、トータルの仕事が
[J]の仕事が出来たはずなのに、妹が仕事をした結果、トータルの仕事が
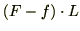 [J]になっているわけですから、妹が車にした仕事は負の仕事で
[J]になっているわけですから、妹が車にした仕事は負の仕事で
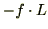 [J]であることがわかってもらえたと思います。
[J]であることがわかってもらえたと思います。
物体の運動方向に加えた力がした仕事は正
運動方向と逆に加えた力がした仕事は負
力を加えてもその方向へ全く動かなければ仕事は0
|




: 仕事はベクトル量?
: 仕事
: 仕事をされたかチェック!
目次
平成20年7月14日
![]() [J]だということはイメージしてもらえたと思います。ではその正負はどのように決まっているのでしょうか?ここで次のような状態を考えてください。
[J]だということはイメージしてもらえたと思います。ではその正負はどのように決まっているのでしょうか?ここで次のような状態を考えてください。
![\includegraphics[width=\textwidth]{worklabel1.eps}](../giffile/work_a_energy/worklabel1.gif)
![\includegraphics[width=\textwidth]{worklabel2.eps}](../giffile/work_a_energy/worklabel2.gif)
![]() [N]を加えて距離
[N]を加えて距離![]() [m]だけ動かしたとき、その力
[m]だけ動かしたとき、その力![]() [N]は物体に仕事
[N]は物体に仕事![]() [J]を与えた」でしたね。妹は車に力
[J]を与えた」でしたね。妹は車に力![]() [N]を加えています。そして車が移動してしまったので、移動距離も発生しています。だったら仕事は当然生じます。
しかし、妹が加えた仕事はお兄ちゃんが加えた仕事とは少々違います。さて何が違うのでしょうか?車の移動方向と、車に加えている力の方向をよく確認してみてください。
[N]を加えています。そして車が移動してしまったので、移動距離も発生しています。だったら仕事は当然生じます。
しかし、妹が加えた仕事はお兄ちゃんが加えた仕事とは少々違います。さて何が違うのでしょうか?車の移動方向と、車に加えている力の方向をよく確認してみてください。
![]() [J]の仕事が出来たはずなのに、妹が仕事をした結果、トータルの仕事が
[J]の仕事が出来たはずなのに、妹が仕事をした結果、トータルの仕事が
![]() [J]になっているわけですから、妹が車にした仕事は負の仕事で
[J]になっているわけですから、妹が車にした仕事は負の仕事で
![]() [J]であることがわかってもらえたと思います。
[J]であることがわかってもらえたと思います。
![\includegraphics[width=\textwidth]{conc3.eps}](../giffile/work_a_energy/conc3.gif)