力学

相対速度・加速度に関する問題

ここからは今まで学んだ「おでん矢印」をどのように問題に適用したらよいのかを学んでいきます。

問1

問1　物体Aに対する物体Bの速度を求めよ。

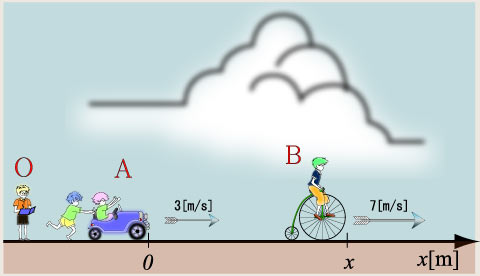**図 13:** Aに対するBの相対速度問2へ戻る

では「おでん矢印」で考えてみましょう。「Aに対する…」ですから基準はAですね。したがって「だいこん」に「A」を、「ちくわぶ」には「地」を、「たまご」に「B」を書きましょう。矢印を書いてください。その後で、地面から見たAとBの速度（もちろんベクトル量ですから軸方向が正ですよ）を書き込みましょう！そうすると「Aから見たBの相対速度」を $v_{AB}$ と書くと

**図 14:** おでん矢印に書き込む

$\displaystyle v_{AB}= 7-3 = 4$ [m/s]

(3)

つまりAから見るとBは4[m/s]で軸方向へ進んでいるように見えるわけです。

△上へ戻る

問2

問2　図13において物体Bに対する物体Aの相対速度を求めよ。

では次に「物体Bに対する物体Aの相対速度」を求めてみましょう。今度は「物体Bに対する…」という文ですから基準が「B」となります。では、「だいこん」にBを書き込みましょう。比較される対象は「A」ですから「たまご」が「A」、静止系は「地」ですね。

矢印を書いたあとで、地面に対するAとBの速度を書きましょう。先ほどと同じでAは3[m/s]Bは7[m/s]ですね。しかし、AとBが交換されてますから気をつけてください。ちゃんと図を描くと、図15のようになります。

**図 15:** おでん矢印に書き込む

つまり

$\displaystyle v_{BA}= 3-7 = -4$ [m/s]

(4)

となります。物体Bから物体Aを見ると、 $v_{BA}$ の符号が負になってますから、軸と逆方向へ4[m/s]の速さ（大きさですね）で去っているように見えるわけです。

次に相対加速度を求めてみましょう。

△上へ戻る

問3

問3　物体Aに対する物体Bの相対加速度を求めよ。

**図 16:** ともに加速度運動

図16の2物体A、Bは共に加速度運動をしています。物体Aの加速度は[m/s]、物体Bの加速度は[m/s]です。最初に述べましたように、相対速度も相対加速度もどちらも同じ解き方で解けます。つまり、単位さえ間違わなければとても簡単なんです。

軸の方向に注意して、基準となる物体はAであることを確認し、おでん矢印に各値を記入していきます。

**図 17:** おでん矢印に書き込む

$\displaystyle a_{AB}=a_2- a_1$ $\displaystyle \mbox{[m/s$^2$]}$

(5)

とっても簡単でしょ？すぐに解りますね。ちなみに式(5)が言っているのは、「物体Bは物体Aから見ると、軸の方向へ[m/s]の加速度で移動しているように見える」ということです。が負の場合は軸と逆方向、正の場合は軸の方向となります。

△上へ戻る

問4

問4 図18のように車が速さ $2\sqrt{3}$ [m/s]で走っているとき、風がない状態で、雨が鉛直方向に対して60°の角度で前方から降ってくるように見えた。雨滴の落下の速さはいくらか。

**図 18:** 雨が降ってきた

さて、典型問題です。これは水平方向と鉛直方向の2軸に分けて考えればすぐに分かります。では考えてみましょう。

雨滴の速さが問われていますので、雨滴の速さを $v_{1}$ として、下向きに設定しましょう。そういえば鉛直方向の軸が設定してありませんね。雨の落下方向を正にしていた方が後々都合が良いですから、下向きを正として軸を設定しておきましょう。

車の速さは与えられていますが方向は与えられていないため、勝手に図18のように右向きに軸を設定しました。では車の速度も軸向きに $2\sqrt{3}$ [m/s]としましょう。また雨の軸方向の速さをとして設定します。さらに、車の軸方向の速さもとして設定しましょう。

問題では「車」から見て「雨」が鉛直方向と60°の角をなしていたので、基準は「車」とした方がよいようです。では軸方向と軸方向、それぞれに対する相対速度を求めましょう。もちろん矢印の方向は軸方向ですよ。

**図 19:** 各軸における相対速度

ここで少々常識が必要となります。

風が無いので、雨は軸方向へ落ちる（軸方向の速度成分はない）
車は軸方向の速度成分のみを持つ（軸方向へは移動しない）

そうしますと[m/s]、[m/s]となりますね。ですから、車から見た雨の軸方向と軸方向の相対速度は

$\displaystyle \mbox{$x$軸方向}$	$\displaystyle : v_x=-2\sqrt{3}$ [m/s]	(6)
$\displaystyle \mbox{$y$軸方向}$	$\displaystyle : v_y=v_1$ [m/s]	(7)

となります。が負になっているのは、車から見て雨滴は、実際は軸方向と逆方向へ速さ $2\sqrt{3}$ [m/s]で移動しているように見えるということですね。そしてここまで出れば後は簡単です。あとは車から見て雨は60°の方向へ移動しているように見えたわけですから、

**図 20:** 車に対する雨滴の相対速度

ちょうど角度30°の三角形が見えます。後は比より $1:\sqrt{3}=v_1:2\sqrt{3}$ より[m/s]と求まりますね。

どうでしょう？相対速度・加速度の考え方は分かっていただけたでしょうか？

△上へ戻る

相対系の問題 | 問1 | 問2 | 問3 | 問4

ホーム＞物理のトップページ＞目次＞力学＞相対速度と加速度＞相対系の問題