力学

相対速度

相対速度とはどのようなものでしょうか？相対…何やら言葉が難しいですか…。でも大したことはありません。何なら易しく言い換えましょう。「相対」とは「相手に対する自分の…」です。つまり、「相対速度」とは「相手に対する自分の速度」です。もちろん逆も成り立ちます。つまり「自分に対する相手の速度」でもOKです。

もちろん速度と言っていますから、ベクトル量を扱うわけです。ベクトル量で大事なことと言ったら…もう再三言って来たから大丈夫ですよね？…そうです。軸です。

相対の意味が原義とは微妙に異なりますが、とりあえずこのように理解していただいて結構です。つまり軸神が設定する正の方向を向いているならば正、逆方向を向いているならば負と扱うわけです。

△上へ戻る

相対速度の具体例

では具体例を挙げて考えてみましょう。

**図 1:** 2物体の運動

今図1のように物体Aが10[m/s]で、物体Bが15[m/s]で共に軸方向へ進んでいるとします。そうすると物体Aから見て物体Bはどのように見えるでしょうか？…車に乗って前の人を見るとどのように見えますか？という質問と全く同様です。ですから、簡単に想像出来ますね。そうです。もちろん5[m/s]で軸方向へ進んでいるように見えます。

でも毎回毎回想像しやすい問題か？というとそうでもありませんし、速度が文字になったときに途端に出来なくなってしまう人が多いのです。ですから、相対系を扱うツールをご紹介します。まずは運動を定義しないとどれとどれの相対速度を扱うのか分かりませんね。では図2をご覧下さい。今度は速度を文字にしました。

△上へ戻る

速度を一般化した相対速度

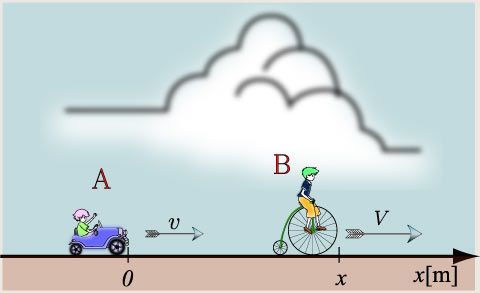**図 2:** 2物体の運動下へ戻る

この図において、Aの速度は[m/s]、Bの速度は[m/s]となります。ここで「Aに対するBの相対速度 $v_{AB}$ 」を考えてみましょう。 $v_{AB}$ は $v_{A\rightarrow B}$ という意味です。Aから見たBの速度ということですね。つまり、「Aに対する…」と言われたら、「Aを基準として…」と読み換えてみましょう。ベクトル量とは即ち「何かを基準としたときの、もう一方の位置と大きさ」を表すものです。ですから相対速度も今までのベクトルの扱い方と何ら変わりませんね。

△上へ戻る

相対系を扱うツール

さて、相対系を扱うツールを紹介するのでした。では、次の図3をご覧ください。

**図 3:** おでん下へ戻る

おでんです。…「ちくわぶ」に「だいこん」に「たまご」と「こんにゃく」…なんて説明は絶対に要らないでしょうが、使い方の紹介の前に構成を説明しなくてはなりませんね。

**図 4:** おでんの構成

実は図4のようになっています。「串」と「こんにゃく」で軸を表しています。手書きのときは当然図4の右に描いたように、最初に○□○と書いて、そのあとで→を後ろに書くという感じで書いて下さい。

△上へ戻る

おでん矢印での処理1

では図2の運動をどのようにおでんで処理するのかをご説明致します。

まずは図3のおでんの各要素「ちくわぶ」「だいこん」「たまご」の中に、運動をしている系の中から必要なものを書いていきます。

**図 5:** おでんの各要素

第一に「ちくわぶ」。この一番ひだりの枠には「静止系」を記入します。基本的には「地面」だと思ってください。図中には面倒なので「地」と書いておきます。

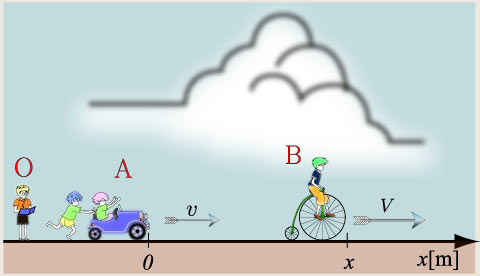
ところで静止系と言われてもよく分かりませんよね。静止系とは、今注目している物体系において止まっていると考えられるものを指します。実際は地球も公転しているわけですが、地球上の物体はすべて地球の等速度運動と共に、同じ等速度運動をしていますので地球上の物体の運動を見る際、地球は止まっているように見えるわけです。ですから静止系は地球となります。イメージし易いように図6に静止系（地球上）における観測者Oを描いておきます。

**図 6:** 静止系のイメージを追加下へ戻る

次に「だいこん」。これはとても重要なのでしっかりと覚えておいてください。皆さんの方は□ですね。この「だいこん」には相対系を処理する「基準となるもの」を書き込みます。今回はAが基準でしたから「A」と書き込みましょう！

最後に「たまご」ですが、これは「基準となるもの」によって「比較される対象」を書き込みます。今回は基準Aによって見られるのは「B」でした。ですから「B」と書き込みます。そうすると図7のような図になります。

**図 7:** 要素を埋め込む

△上へ戻る

おでん矢印での処理2

では次に静止系（O）から見た各物体の速度を考えるために、まずは「ちくわぶ」から各物体を表すおでんの「要素」に弧を描くように矢印を書きます。さらに、注目している基準となる物体Aからも比較される対象Bに対して矢印を書いておきます。すると図8のようになります。当然これらの矢印は軸の正方向を向いている矢印です。

**図 8:** 静止系からの矢印を書く

△上へ戻る

おでん矢印での処理3

ここで、静止系（O）から見たそれぞれの物体の速度とを対応する矢印の弧の部分に書き入れます。Aは速度、Bは速度でしたね。もし図6においてやが負方向を向いていればここでやと書き込むところですが、今回はどちらも軸の方向を向いていますので問題なくやと代入します。

**図 9:** 矢印に値を書き込む

この弧を描いた矢印は実際はベクトル量でして、図10の右の図のようになっています。

**図 10:** 各矢印の関係

つまり $v + v_{AB}$ がと等しくなっているわけです。ですから当然式で書くと

$\displaystyle v + v_{AB} = V$

(1)

となります。式(1)からすぐに $v_{AB}=V-v$ と求まりますね。でもそういう式変形を考えなくても図9を見れば一発でわかるわけです。大きい矢印（）は小さい矢印（と何も書いてないもの）を二つ足したものですから、小さい矢印の何も書いてない残り方は、大きいもの（）から小さい方（）を引けばいいですね！

$\displaystyle v_{AB}= V - v$

(2)

ですから、すぐに図11のように書き込みます。

**図 11:** 残りの値を書き込む

さて、実はこれで既に相対速度が求まっています。図11の「だいこん」から「たまご」への矢印は今求めたい「Aに対するBの相対速度」ですね。Aを基準に見てますから。ですから、Aに対するBの相対速度 $v_{AB}$ はだとわかります。皆さんは手書きで書きますので、図12のようになったはずですね。

**図 12:** 手書きの場合

実は相対加速度も全く同じ考え方ですので、「相対速度・加速度」に関するお話はここで終わりです。しかし、ちゃんとこの「おでん矢印」が使えるかどうか心配ですよね？ですからいくらか問題を出したいと思います。

△上へ戻る

トップページへ | 物理トップページへ | アーカイブス | 次へ：相対系の問題 | 戻る：相対速度トップ

ホーム＞物理のトップページ＞目次＞力学＞相対速度と加速度＞相対速度・加速度