力学

加速度とは

加速度とは何でしょう？加速する度合いですか？そうではありません。加速度という単語を適切に切ると「加える速度」ですね。漢文口調にするなら「速度を加ふ」ですが…。ですから定義はこうなります。「1秒間に変化する速度の変化量」のことを加速度と言います。

次元解析

おそらく微妙に解らないと思っている方も多いでしょうね。ですから、単位から考えてみましょう。学校で加速度の単位は習っていると思います。[m/s]ですね。しかしこのままだとよく解らないんですよ…そこでちょっと式変形したいと思います。

$\displaystyle \mbox{[m/s$^2$]}$	$\displaystyle = \mathrm{\frac{m}{\ s^2\ }}$
	$\displaystyle = \mathrm{\frac{m/s}{s}}$	(1)

式(1)の式変形は分かるでしょうか？m/sはm/sをsで割ったものです。つまり式(1)のように表せます。式(1)をご覧になったら分かるように、つまり1秒間あたりに速度がどれだけ変化したかを表していることが分かりますね。だって、割り算の定義に飛びますか？分数は分母の基本単位量1（今回は1秒）に対する分子の割合ですから。

したがって、最初に定義したように加速度の定義は「1秒間に変化する速度の変化量」となるわけです。速度のときもそうですが、（これからもずっとそうですが…）加速度の定義なんて偉そうなことを言っていますが、単位を読んでいるだけに過ぎません。

つまり、単位に定義が書いてあるわけです。ということは単位が語る内容はとても重要ということになります。だってこれから単位さえちゃんと読めれば、そこから推察して問題を解くという方法をとることも出来るわけですから。

△上へ戻る

重要なポイント

ではここから大事なお話をしましょう。加速度の定義をもう一度ご覧下さい。「1秒間に変化する速度の変化量」ですね。ここには重要なキーワードが隠れています。それは「速度」です。1秒間あたりの速さではなく「速度」なのです。

速度は当然ベクトル量ですから、つまりその変化量を扱う加速度もベクトル量となるわけです。

スカラー量の変化量を扱えばそれがベクトル量になるわけではありません。例えば身長に関してちょっと考えて見ますか？7月に170cmだったのが11月に174cmになったとしましょう。その変化量は $\Delta x = 174 - 170 = 4$ cmとなります。これはただの幅です。あくまで大きさですからスカラー量でしかありません。つまり、単にスカラー量の変化量をとってもそれがベクトル量になるわけではないわけです。

しかし、これを次のように考えます。人が地面に対して正立したとき地面を基準点0として地面に垂直に軸をとります（このルールがとても大事です）。では変化量を見てみましょう。 $\Delta x = 174 - 170 = 4$ cmですね。これはベクトル量です。何故かというと方向が設定してあるからです。正確には基準点0を決めて方向を示す軸を決めたら、その軸上の値はすべてベクトル量ということになりますね。従ってベクトル量かどうかの判断は結局「向き」と「大きさ」が設定してあるかどうかを確認すればよいということですね。

では、お話を戻しまして、「加速度もベクトル量」です。つまり、「大きさ」と「向き」を持った量です。ただし、加速度の大きさを特に別の呼び名で呼んだりはしません。つまり加速度の大きさはそのまま「加速度の大きさ」と言います（速度との対応関係を確認してくださいね）。

△上へ戻る

一般化して考える

では加速度を式を用いて表してみましょう。そのためには図を示さなくてはなりませんね。

**図 1:** 物体の移動

高校物理では等加速度運動しか扱いません。つまり一定の加速度で変化する運動のみを扱うということですから、大学で習うような微分方程式を解く必要がないということです。そこで、図1の運動は等加速度運動をしている物体についての図と考えてください。

そうすると、時間変化 $\Delta t$ は $\Delta t =t - 0$ [s]ですね。その間、物体（車）は1秒間に決められた割合で速度を増しています（等加速度運動）から、速度変化 $\Delta v$ は $\Delta v = v - v_0$ [m/s]となります。そうしますとこの物体の加速度は

$\displaystyle a = \frac{\Delta v}{\Delta t}$	$\displaystyle = \frac{v- v_0}{t - 0}$
	$\displaystyle = \frac{v- v_0}{t}$ $\displaystyle \mbox{[m/s$^2$]}$	(2)

ということになります。これが1秒間あたりの物体の速度変化になります。ですから、今[s]としたときの物体の速度が[m/s]ですから、3秒後はに $\frac{v- v_0}{t}$ を3倍したものを加えたもの $v_0 + 3\times \frac{v-v_0}{t}$ が3秒後の物体の速度に、10秒後は $\frac{v- v_0}{t}$ を10倍したものをに加えたもの $v_0 + 10\times \frac{v-v_0}{t}$ が10秒後の物体の速度になります。

当然秒後の速度はに $\frac{v- v_0}{t}$ を倍したものを加えますから $v_0+t \times \frac{v-v_0}{t}=v_0 + v- v_0=v$ となり、ちゃんと秒後の速度[m/s]になりますね。

△上へ戻る

時の神出現！

ところでちょっと不安に思ったのですが、もしかして[s]のイメージって大丈夫でしょうか？[s]というのは別にその瞬間から止まっていた物体が動き出さなくてはならないわけではありません。誰かが物体の運動を見ていて「時間を計り始めよう！」と決めたその瞬間の時間を[s]と表します。…イメージが掴みづらいですか？…では軸神に次いで時間を刻む神として時の神を出現させますか…。図2をご覧ください。

**図 2:** 時の神出現

時の神は水晶の上に座っている女の子です。彼女が持ってる木の枝で水晶をたたくと時計が動き始めます。彼女はの点を物体が通過した瞬間に時計を動かし始めます。計測中は時計の針が動いていますね。

大丈夫でしょうか。[s]が言っている意味を取り間違えると、いつになっても物理ができるようにはなりません。ちゃんと読み取ってくださいね。

△上へ戻る

具体例にて

では具体例を用いて加速度を求めて行きましょう。折角「時の神」に出て来てもらいましたから、今後も時間は彼女に描画してもらいましょう。では最初の問題です。

問1　次の物体の加速度を求めなさい。

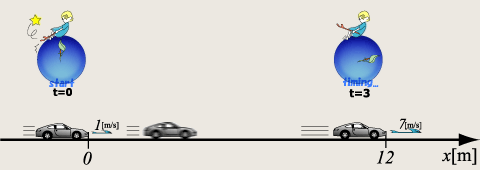**図 3:** 下へ戻る加速度を求める

どうでしょう？速度のところでもお話しましたが、加速度もベクトル量ですよね？これから求めたい加速度はもちろんベクトル量の未知数ですから…守らなければならないルールがありました。それが「ベクトル量の未知数は必ず軸方向へ向ける」でしたね。では軸神やこれから定義すべき加速度矢印も書き込んだ図を示します。

**図 4:** 必要なものを書き込んだ図

何やら踏ん張っている感じの矢印が加速度です。物理全体のイラストの方向性を同期させたため、加速度矢印も変わってしまいました。これからずっとこの矢印を使いますのでここで意識しておいてください。頑張って速度を大きくしている様子を表したらこんな矢印になりました。…それはさておき、当然軸神が示している方向が正なわけですから、加速度矢印は右を向いています。大きさは[m/s]ですね。では必要な値を出して行きましょう。

まずは時間変化量 $\Delta t$ ですが、 $\Delta t = 3 - 0$ [s]となります。次に速度変化量 $\Delta v$ は $\Delta v = 7 - 1$ [m/s]となります。したがって

$\displaystyle a = \frac{\Delta v}{\Delta t }=\frac{7 - 1}{3 - 0}=\frac{6}{3}=2$ $\displaystyle \mbox{[m/s$^2$]}$

(3)

となりました。軸の方向へ[m/s]の加速度です。では次の問題へ行きましょう。

問2　加速度を求めなさい。

**図 5:** 加速度を求める

もう当然、軸に注目しましたよね？加速度はベクトル量ですよ！ですから、軸神と加速度ベクトルの方向を示すと図6のようになります。

**図 6:** 必要なものを書き込んだ図

もう明らかですよね？では時間変化 $\Delta t$ を求めてみましょう。 $\Delta t = 3 - 0$ [s]です。さらに速度変化量 $\Delta v$ は、速度がベクトル量なので軸神の言う方向を正と捉えていることを頭に置いて $\Delta v = -7 - (-1)$ [m/s]となります。分かりますか？ベクトル量の未知数はもちろん軸神の言う方向にそろえるわけですが、当然普通の速度もベクトル量ですから、軸神からみて正なのか負なのかが決まるのです。ですから当然[s]のときは軸神が言う方向と逆方向を向いて[m/s]なわけですから、[m/s]と表されます。つまり

$\displaystyle a = \frac{\Delta v}{\Delta t }=\frac{-7 - (-1)}{3 - 0}=\frac{-6}{3}=-2$ $\displaystyle \mbox{[m/s$^2$]}$

(4)

となります。軸の方向と逆方向に[m/s]ということですね。

問3　加速度を求めなさい。

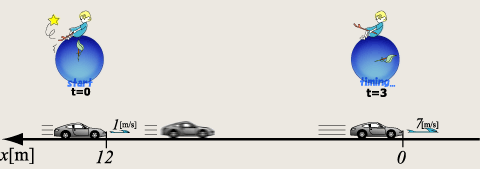**図 7:** ちょっと下へ戻る加速度を求める

もう大丈夫ですよね？軸方向に気をつけてください。では加速度ベクトルと軸神を付け加えた図を考えてみましょう。

**図 8:** 必要なものを加えた図

当然加速度ベクトルをちゃんと軸神の方向へ向けましたよね？では時間変化 $\Delta t$ です。 $\Delta t = 3 - 0$ [s]となります。これはもう大丈夫ですね。時間は戻ることなど決してありませんし…。では次に、速度変化 $\Delta v$ を考えてみます。 $\Delta v = -7 - (-1)$ [m/s]となります。軸方向を正しくチェックしてくださいね。

$\displaystyle a = \frac{\Delta v}{\Delta t }=\frac{-7 - (-1)}{3 - 0}=\frac{-6}{3}=-2$ $\displaystyle \mbox{[m/s$^2$]}$

(5)

そうすると符号が負の[m/s]になってしまいました。これは軸と逆方向へ速さ 2[m/s]で移動という意味ですね。

もちろんお気づきでしょうが、図7の物体の運動は図3と全く同じ運動です。ただ、私が勝手に軸の設定を決めただけですから、符号が逆になるだけで、同じ内容を示す答えになっています。よく見比べてください。

では最後に

問4　加速度を求めなさい。

**図 9:** 加速度を求める

そろそろ間違うことが無くなって来たでしょうか？では加速度ベクトルと軸神を付け加えた図を考えてみます。

**図 1:** 必要なものを加えた図

おさらいしておきますね。まずは軸神をチェック。その方向へ未知のベクトル量を設定（出題者から設定されてしまっているベクトル量…例えばのときの速度1[m/s]等は変えませんよ）。そして時間はかならず増える方向にしか進みませんから、時間を確認して進んでいる方向を確認。そうしたら、変化量を求めるわけです。

では時間変化 $\Delta t$ です。 $\Delta t = 3 - 0$ [s]となります。これは間違うはずがありません。では次に、速度変化 $\Delta v$ を考えてみます。 $\Delta v = 7 - 1$ [m/s]となります。与えられた[m/s]や[m/s]の速度が正なのはどちらも軸の方向を向いてるからですね。

$\displaystyle a = \frac{\Delta v}{\Delta t }=\frac{7 - 1}{3 - 0}=\frac{6}{3}=2$ $\displaystyle \mbox{[m/s$^2$]}$

(6)

△上へ戻る

まとめ

もちろんまだ色んなパターンがありますが、もうそれも全て解けるはずです。それはこの速度や加速度を求めるルール

未知数のベクトル量は軸向きに定義する
出題者が決めたベクトル量はその方向のままにして、式で考えるときに正負を考える

を理解したからです。「原理」さえ理解できれば解けない問題はなくなります。なぜなら出題者は「原理」から問題を作成するからです。「原理」的におかしいことは問題にできませんから。

しっかり復習してくださいね。

△上へ戻る

ホーム＞物理のトップページ＞目次＞力学とは＞加速度とは