力学

運動をv-tグラフへ

では実際に運動をグラフに変換してみましょう。次の運動をご覧下さい。

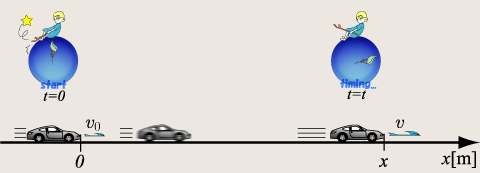**図 3:** 等加速度運度下に戻る

物体（車）がちょうど[m]を通過したときの時間を[s]に、そしてそのときの速度を[m/s]とします。x=x[m]やt=t[s]等の表現は大丈夫ですよね？最初の文字xやtが物体の位置や時間の変数を表し、次の文xやtが、そのときの具体的な値を示しています。x=x[m]を例に取りますと、「物体がある位はx[m]です」という意味になります。そのまま等加速度運動をした物体は[m]の位置に達したとき[s]で、そのときの速度を[m/s]となりました。これをグラフに描いてみましょう。

**図 4:** v-tグラフ化

解るでしょうか？…もしかしたらこのように、運動からグラフに変換するのが苦手な人も多いかも知れませんね。…今回は最初なので、丁寧に変換の仕方を見ていきましょう！flashコンテンツによるv-tグラフシミュレーションのページがあります。そちらへ飛びますか？

△上へ戻る

v-tグラフの作り方

まずは、これから作るグラフの軸が示す変数の値を確認します。今回は縦軸が[m/s]、横軸が[s]となります。

**図 5:** 下に戻る軸の変数に注目

次に物体が運動している図を確認します。グラフの横軸は時間[s]ですから、運動における時間を確認しますと、

**図 6:** 時間の確認

図6のように[s]と[s]と解ります。ですから図5にその値を書き込みましょう。

**図 7:** t軸に運動の時間を書き込む

今回は原点で[s]は分かるでしょ？という意味を込めて[s]は書かずに、[s]だけを書き込みました。

さて次に縦軸に移りましょう。さきほど確認しましたように、グラフの縦軸は[m/s]軸ですから、図3の運動から[s]のとき[m/s]、そして[s]のとき[m/s]ということがわかります。時間（横軸）との対応関係もしっかりと確認して下さいね。

**図 8:** 時間に対応する速度のチェック

では、これもグラフの縦軸に記入しましょう。…！！？すっかり言うのを忘れてました！実は大事なお話がありました。もう当然意識しているとは思いますが、速度はベクトル量です。ですからグラフの軸の正の値は当然「運動の図」の軸神が決める正を表します。今回はどちらも正の方向を向いてますので、グラフにおいても正の値として記入します。ベクトル量の正の方向のお話はもう大丈夫ですよね？

**図 9:** v軸に時間に対応した速度を書き込む

これで各軸の値がわかりました。では、それぞれの交点を求めて、グラフを完成してみます。

**図 10:** v-tグラフ完成

△上へ戻る

v-tグラフと運動の関係

グラフと運動の関連を見てみましょう。

**図 11:** v-tグラフと運動の関係

ちょっと丁寧すぎましたか…。しかし以後は同じようにやることを前提で、いきなり図を描きますから、しっかりと理解しておいてくださいね。

△上へ戻る

運動をv-tグラフへ | 変換の仕方 | グラフと運動の関係

ホーム＞物理のトップページ＞目次＞力学とは＞ v-tグラフ＞グラフ変換