 _MASTER'S EYE
_MASTER'S EYE
では、皆さんは図12からどのようなものが読み取れるでしょうか?
もちろん![]() 軸の
軸の![]() [s]や
[s]や![]() [s]、さらに
[s]、さらに![]() 軸の
軸の![]() [m/s]や
[m/s]や![]() [m/s]も読み取れるでしょう。しかし、それ以上にこのグラフには有用な情報が隠れています。ではそれを考えていきましょう。
[m/s]も読み取れるでしょう。しかし、それ以上にこのグラフには有用な情報が隠れています。ではそれを考えていきましょう。
ここで、もう一度数学の「直交座標」に登場してもらいます。
今回は直交座標内に直線を引きました。さてこの直線の傾き![]() はどのように表されるでしょう?
はどのように表されるでしょう?
ですよね。![]() は変化量を表します。つまり
は変化量を表します。つまり![]() であれば「
であれば「![]() の変化量」という意味になります。
の変化量」という意味になります。
この傾きがどのくらい有用なのかはいつか数学の方で語ることにしまして、では物理における![]() グラフの傾きはどのようになるのでしょうか?
グラフの傾きはどのようになるのでしょうか?
もちろん軸が![]() ではなく
ではなく![]() ですから、傾きは
ですから、傾きは
となります。これを見て何か思い出すことはありませんか?…速度変化を時間変化で割ったもの…。つまり「1秒間あたりの速度変化」…そうです。加速度ですね。すなわち![]() グラフにおける直線の傾きは「加速度」を表すわけです。
グラフにおける直線の傾きは「加速度」を表すわけです。
せっかくですから、グラフ中にある値を使って、この運動の加速度を求めてみましょう!
となりました。この式(5)は後で使いますのでしっかり覚えておいて下さい。
![]() グラフの傾きがそのときの運動の加速度を表すことがわかりました。しかし
グラフの傾きがそのときの運動の加速度を表すことがわかりました。しかし![]() グラフからわかることはそれだけではありません。では他にどのようなことが読み取れるのでしょうか?次の運動をご覧下さい。
グラフからわかることはそれだけではありません。では他にどのようなことが読み取れるのでしょうか?次の運動をご覧下さい。
普通の速度![]() [m/s]での等速度運動です。これを
[m/s]での等速度運動です。これを![]() グラフで表すと
グラフで表すと
となります。…ここで小学生のときからずっとやって来てますよね。等速![]() [m/s]で
[m/s]で![]() [s]間進んだときの距離はどれだけになるでしょう?
[s]間進んだときの距離はどれだけになるでしょう?
おそらく意味もわからず「はじき」だの「みはじ」だの言って覚えている方も多いでしょうが、これからはちゃんと単位で読み取ってくださいね。速度というのは「1秒間にどれだけの距離進むかを表す値」というのが定義ですから、![]() 秒間で進んだ距離が知りたいのならば、その
秒間で進んだ距離が知りたいのならば、その![]() に
に![]() をかければいいだけの話です。そうすると
をかければいいだけの話です。そうすると![]() 秒間で進んだ距離が分かります。式(5)の単位表記を見ていただけば、一目瞭然ですね。
秒間で進んだ距離が分かります。式(5)の単位表記を見ていただけば、一目瞭然ですね。
ではその![]() 秒間で進んだ距離は、図18においてどこに現れてくるのでしょう?進んだ距離
秒間で進んだ距離は、図18においてどこに現れてくるのでしょう?進んだ距離![]() は式(5)のように表されていますから…
は式(5)のように表されていますから…
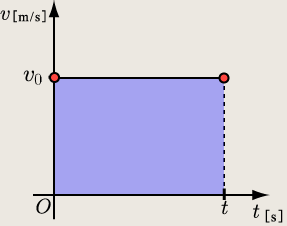 |
図19のように表されますよね。
![]() で表される距離
で表される距離![]() は
は![]() グラフにおいて面積で表されます。これは、実際には微小時間
グラフにおいて面積で表されます。これは、実際には微小時間![]() 秒間に進んだ距離
秒間に進んだ距離
![]() を時間0[s]から
を時間0[s]から![]() [s]まで加え合わせたものになります。
[s]まで加え合わせたものになります。
では、今回の運動の場合を考えてみましょう。もう一度今回の等加速度運動の図を出します。
前は兄妹のところが車でしたちょっと図を変えてしまいました。こっちの方が、穏やかな感じでやわらかいから物理が楽しくなぁ…とか思ってではなく、時の神が少々浮いている間があったので、全体をそちらに合わせたというのが本音ですが…。この図の構想から作図までに6時間ほどかかってしまい…そのせいで自宅でのノルマに影響が…
さて、妹を後ろから押して加速してあげるお兄ちゃんの図ですが、もちろん彼には等加速度運動をやってもらいます。ちょっと辛いですけどね(^^;)
図19と図20で学んだように、![]() グラフにおいて微小時間での
グラフにおいて微小時間での
![]() の和は進んだ距離になります。ですから
の和は進んだ距離になります。ですから
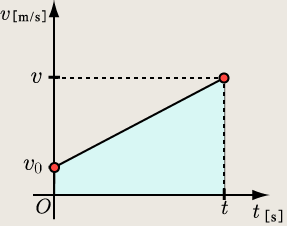 |
これはすぐに解るでしょうか?さっきの微小時間に進む距離の和がトータルで進んだ距離の和というのを思い出してみましょう。
図24のように、微小時間![]() の間に進んだそれぞれの距離
の間に進んだそれぞれの距離
![]() [m](
[m](![]() はその時々の速度)の和を
はその時々の速度)の和を![]() [s]から
[s]から![]() [s]までとるとその間に進んだ距離を表します。ここで図24においてちょっと直線からはみ出した領域が気になる人がいるかもしれませんが、それは
[s]までとるとその間に進んだ距離を表します。ここで図24においてちょっと直線からはみ出した領域が気になる人がいるかもしれませんが、それは![]() を限りなく小さくしたら全く問題なくなりますね。だって、はみ出す部分は近似的になくなりますから。だから結果図23の領域になることは理解できますね。
を限りなく小さくしたら全く問題なくなりますね。だって、はみ出す部分は近似的になくなりますから。だから結果図23の領域になることは理解できますね。
ではその![]() [s]から
[s]から![]() [s]までの間に進んだ距離を求めてみましょう。
[s]までの間に進んだ距離を求めてみましょう。
求める際は以下のように面積を二分します。
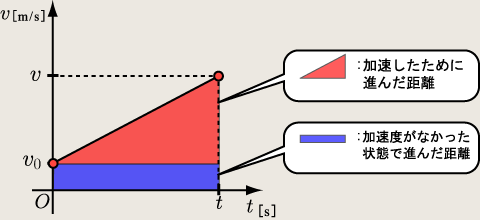 |
青の領域は等速で進んでいたときの距離![]() [m]です。これは前に図19でも示しましたね。アレと同じです。そして赤の領域は加速をしていたせいで余計に進んでしまった距離
[m]です。これは前に図19でも示しましたね。アレと同じです。そして赤の領域は加速をしていたせいで余計に進んでしまった距離![]() [m]です。この領域が図19に加えられるのです。ではその二つの和
[m]です。この領域が図19に加えられるのです。ではその二つの和![]() [m]を出してみましょう。
[m]を出してみましょう。
ここでもう一度式(4)を思い出してください。
![]() でしたから、式(8)中の
でしたから、式(8)中の![]() は
は
![]() と書けますね。ですから式(8)は
と書けますね。ですから式(8)は
となります。ちなみに、式(5)は変形して![]() を求める式にすると
を求める式にすると
と書けます。この2つ何やら見覚えのある方も多いかと思います。…というか見覚えがないとダメです。力学の基本3公式(こう言ってるのって私だけ?)のうちの2つですね。では3つ目はどうするかと言いますと…式(9)と(10)を連立させて![]() を消去するんです。式(10)より
を消去するんです。式(10)より
![]() ですから
ですから
式(11)では、分子にそれぞれ![]() があるからそれを共通項としてくくっています。計算が楽になりますね。ということで式(12)になります。ではこの式(12)の分母をはらってみましょう。
があるからそれを共通項としてくくっています。計算が楽になりますね。ということで式(12)になります。ではこの式(12)の分母をはらってみましょう。
という式が出てきます。これは結局式(9)と(10)から![]() を消去した式なので、
を消去した式なので、![]() がわからない状態で
がわからない状態で![]() や
や![]() 、
、![]() や
や![]() のどれか3つが解っているときに、
のどれか3つが解っているときに、![]() を求めなくても使える式として、わざわざここで出していますが、結局「力学的エネルギー保存則」を習うとそれと同じことなので、わざわざ覚えるのもなぁ…と思います。
を求めなくても使える式として、わざわざここで出していますが、結局「力学的エネルギー保存則」を習うとそれと同じことなので、わざわざ覚えるのもなぁ…と思います。
物理を公式でどうにかしようというのは無理なお話です。問題を解くときには現象を把握し、それを自分で式にしなくてはなりません。だから難しいと言われるのでしょうが、逆にどうしてその公式が出てきたのかというのを覚えておくと、それを使う理由もわかるので、すぐに問題が解けるようになります。一緒に頑張っていきましょうね!flashコンテンツによるv-tグラフシミュレーションのページがあります。そちらへ飛びますか?
右にflashで作ったv-tグラフシミュレーションへのリンクがあります。そちらから飛ぶと、今学んだv-tグラフを自分で作って直にv-tグラフと実際の動きとの感覚的マッチングを取ることができます。是非ご利用ください。
ということで現時点ではとりあえず式(13)も大事だということにしておいて
は覚えておいてください。あぁっと、意味の確認をするのを忘れていました。
![]() は、加速度さえなければ速度
は、加速度さえなければ速度![]() は
は![]() のままであったことを意味します。加速度があると、加速度とは「1秒間にどれだけ速度が変化するか」という値ですから、
のままであったことを意味します。加速度があると、加速度とは「1秒間にどれだけ速度が変化するか」という値ですから、![]() 秒間で変化する量は当然
秒間で変化する量は当然![]() [m/s]になります。ですから結局加速度
[m/s]になります。ですから結局加速度![]() があると、
があると、
![]() となります。
となります。
さらに、
![]() ですが、これは図25でお伝えしたので大丈夫でしょう。加速度がなかったら
ですが、これは図25でお伝えしたので大丈夫でしょう。加速度がなかったら![]() になりますが、加速度があるせいで余計な三角形の部分の面積だけ進んでしまうので、それを加えて
になりますが、加速度があるせいで余計な三角形の部分の面積だけ進んでしまうので、それを加えて
![]() となります。
となります。
3つ目の式は先ほども言いましたように、ただ上2式から![]() を消去しただけです。これらの使い方は後々問題演習のページを作るかも…知れません。まぁ、皆さんの要求次第です。
を消去しただけです。これらの使い方は後々問題演習のページを作るかも…知れません。まぁ、皆さんの要求次第です。
ホーム > 物理のトップページ > 目次 > 力学とは > v-tグラフとは > v-tグラフから読み取れるもの