力学

速度とは

いきなりですが、速度の定義、きちんと言えるでしょうか？…「速さ」と混同してたりしませんか？きっと焦った人いますよね？その人はもう入口からこけてますよ？今からしっかり理解しましょう！

速度の定義

速度とは「物体がある時間にどれだけ移動したか」を表す量です。物理では基本的にMKSA単位系（Mはメートル、Kはキログラム、Sは秒、Aはアンペアの意）を用いますので、速度を正確に表すと「物体が1秒間あたりどれだけの距離（m）移動したか」という量になります。

では次の図1をご覧下さい。

**図 1:** 物体の移動

0[s]のとき[m]のところにいた車は[s]のときに[m]のところにいます。この車は最初から等速で走っているとします。つまり、左から走ってきてその途中で[m]のところを通過したときを[s]としたわけです。

ここでΔx=L-0等の考え方を出しましたが、これが良くわからない人は、ベクトル量の考え方が良くわかっていません。是非「ベクトル量とは」のページをご参照ください。（現在はまだこのページを作っていません）では、速度[m/s]を求めてみましょう。はvelocity（速度）のです。定義から速度は「物体が1秒間あたりどれだけ移動したか」でしたから、今位置からまで移動した距離 $\Delta x$ が $\Delta x = L - 0$ [m]そして、その間にかかった時間が $\Delta t = t - 0$ [s]なので、

$\displaystyle v$	$\displaystyle = \frac{移動した距離}{かかった時間}$
	$\displaystyle = \frac{\Delta x}{\Delta t} = \frac{L - 0 }{ t - 0 } = \frac{L}{t}$	(1)

となります。

割り算の定義へ飛びますか？ここで、大事なことは結局式(1)で求めた値は単位が[m/s]となりますので、割り算の単位の定義から1秒間あたりの移動距離であるということです。ここ、当たり前じゃん…と飛ばされそうですが、実はとても大事なお話です。秒間かかって移動したときの速度を求めましたが、結局その秒間移動というものは1秒間あたりに直されているわけです。

文字じゃよくわかりませんか？という形では残ってるじゃん！と言われそうですね…。では具体的に値を入れて考えてみましょう！

△上へ戻る

具体的な例で考える

図2のように[m]を通過するときの時間が[s]で、そのまま等速で進み[m]を通過するときの時間が[s]であるとします。

**図 2:** 具体的な物体の移動

$\displaystyle v$	$\displaystyle =\frac{20 - 0}{4- 0}$
	$\displaystyle =5$ [m/s]	(2)

4秒間における移動量の変化を求めたのに1秒あたりの移動量の変化に変わりましたね。わかりますか？4秒間で20[m]進むことはつまり1秒間で5[m]進むことを意味していたわけです。平均化しているわけですが、この1秒あたりの値が求まるということがとても大事な意味を持っています。さてそれは何故でしょう？

1秒あたりの移動距離を求める(速度[m/s])と、その結果その割合で進んだときに、何秒後であっても瞬時に移動距離を求めることができるからなんです。

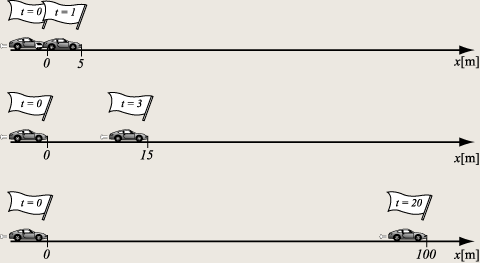
例えば式(2)のように速度が5[m/s]であった場合、1秒では当然5[m]進みますし、3秒だったら15[m]、20秒だったら100[m]進むことが分かるわけです！もちろん雰囲気ではなく、掛け算で求めますよね。とても便利です！だからわざわざ1秒あたりの移動距離として定義しているわけです。

単位を見てください！速度の単位は[m/s]となっていますから、ここに時間[s]を掛けると[m/s] $\times$ [s]= [m]となりますよね。だから距離が求まるわけです。単位から考えても分かりますね。これを次元解析と呼びます。次元とは単位の種類の違いのことです。kgとgは同次元のMと表されます。また時間はT、長さはLとなります。だから式(3)は正しくは[LT ^-1T]=[L]なんでしょうが、まぁここでは良しとします。

$\displaystyle \mathrm{\frac{m}{s}\times s = m}$

(3)

下に、それぞれの例に対応する図を示します。

**図 3:** 時間に対応する移動距離

△上へ戻る

とても重要なお話

実はまだ、大事な話があります。ここを疎かにすると…きっとあなたは物理をずっと中途半端な公式に頼って解いていかなくてはならなくなるでしょう。それくらい大事な部分です！

その大事な話とは…「速度はベクトル量」ということです。ベクトル量？…などと思っている人はいませんか？これってとても大事なお話なんです。「な～んだ。そんなこと知ってるよ。」なんて思っている人…恐らくきっと認識があまいですよ？この「速度はベクトル量」という定義、実はあなたが思っているほど適当に流していい定義ではないんです！これをちゃんと認識しているかどうかで物理の不可解が無くなるか無くならないかが決まるんです！

では説明します。まずはベクトル量から。ベクトルが「向きと大きさを持つ矢印」ですから、ベクトル量は「向きと大きさを持った量」ということになります。つまり速度はどの向きに1秒間にどれだけ移動するかを示さなくてはならない値だということです。つまり表している値が2つあるわけです。向きと大きさですね。

ベクトル量と対応関係を持つ「スカラー量」に関しては「ベクトル量とは」のページに譲ります。では、ここからがとても大事なんですが…、実は物理においてベクトル量の（方向の）正負を決めているのは軸なのです！「なんだ…そんなこと？」とか思っている人いるでしょ！きっとその理解は中途半端ですよ！このお話、超重要です！

△上へ戻る

軸神登場

私から言わせると物理において「軸は神様」です。

**図 4:** 軸は物理において神様

とりあえず図4に神様を出現させておきました。この神様（軸神）が右向きが正と言っているわけです。軸神が言うんだったら仕方ないですね。だから右向きが正です。

しかし問題において「軸神が右向きを正としました」なんてコメントはありませんよね。では、誰が決めるのでしょう？…もちろん皆さんではありません。出題者が決めるのです。出題者が決めた軸に軸神が宿るわけです。

何故出題者が軸を決めるか疑問に思った人はいますか？それは当然、「軸を決めなければベクトル量の値が人それぞれに正だったり負だったり、はたまた別方向を向いてたりするから」です。言い換えると皆さんが好き勝手に軸を設定されたら答えが一つにまとまらずに○付けが大変だからということです。

では戻りまして、何故軸神が方向を決めることがそれほど大事なのかといいますと、実はこれから皆さんが習うもちろん学校で習ったでしょうけど…

$\displaystyle v$	$\displaystyle =v_0 + at$	(4)
$\displaystyle x$	$\displaystyle =v_0t + \frac{1}{2}at^2$	(5)

という式は実はベクトル方程式だからです。

ピンときませんね？なぜならそういう風に方向を意識した方程式だということを習ってないからです。その意識の無さが結局問題が解けないことに現れてくるのです。公式を作った人は適当に作ったわけではありません。ちゃんと、意識するものは意識して、概念を式に表しなおしたものが公式なのです。ですから式(4)も式(5)も共に軸の方向を意識して定義されているのです。

△上へ戻る

ベクトル量の未知数

ここで、さらに大事なお話を加えます。それは「ベクトル量の未知数を求めるときは、その未知数は必ず軸の正の方向に向ける」というものです。

ベクトル方程式の内容理解を私なりの言葉に変化させてお伝えしているわけですが、もちろんベクトル量の未知数というものがよくわかりませんよね。

未知数とはわからない量のことを言います。わからない量…それは即ちこれから求めたい量です。それは式(4)のや、のことを指します。つまり「ベクトル量の未知数を求めるときは、その未知数は必ず軸の正の方向に向ける」とは、やの値が軸神が決めた正の向きを向いているわけです。

△上へ戻る

ここまでのまとめ

説明だけだときっとよくわからないことでしょう。ですから、これまでの話

ベクトル量とは「大きさと向きを持った量」のこと
ベクトル量の正負を決めるのは軸神
ベクトル量の未知数は必ず軸の正方向向きに定義されている

を頭に入れながら次の例題をやってみましょう。

△上へ戻る

例題

問1.速度を求めよ。

**図 5:** 速度を求めよ
下に戻る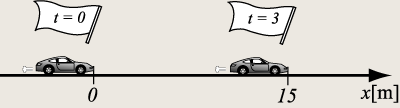

どうですか？求めることが出来ましたか？これは軸神と、求める速度を書き込むと次の図6のようになります。

**図 6:** 軸神と速度矢印付加

今から求める速度は当然まだ決まってない速度です。ということは「未知数」ですね。ですから軸神が定める正の方向に向けて定義します。つまり図6のように右向きに向きます。（これはきっと車の移動方向を見ても感覚的にわかるので問題ないと思います）

では、速度を求めてみましょう！図6より、時間変化 $\Delta t$ は $\Delta t = 3 - 0$ [s]で、移動距離 $\Delta x$ は $\Delta x = 15 - 0$ [m]ですから、

$\displaystyle v = \frac{\Delta x}{\Delta t}= \frac{15}{3}= 5$ [m/s]

(6)下に戻る

となります。つまりこの速度[m/s]が言っていることは、「物体（車）は軸の方向へ1秒間あたり5mの割合で移動している」ということです。

では次の問題を解いてみましょう。

問2　速度を求めよ。

**図 7:** 速度を求めよ

さて、解けますか？これも軸神と速度を図中に書き込んでみましょう。

**図 8:** 軸神と速度矢印付加

きっと速度の矢印を左向きにした人がいますよね？それ、間違いです。「えぇ、どうして？車は左に動いてるじゃん！」とかいうクレームが聞こえてきそうですが、最初に言いましたよね？公式ではなく、物理にもちゃんとルールがあるんです。そのルールが「軸神」です。

そう…ちゃんと軸神が右を正にしろと言っています。ですから、誰が何と言おうと右向きが正なんです。そして、これから求める速度は当然「未知数」ですから、「ベクトル量の未知数を求めるときは、その未知数は必ず軸の正の方向に向ける」というルールにより、かならず右方向に設定しなくてはならないわけです。

では速度を求めてみましょう。時間変化 $\Delta t$ は $\Delta t = 3 - 0$ [s]です。そして変位 $\Delta x$ は $\Delta x = 0 - 15$ [m]です。ですから

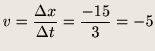$\displaystyle v = \frac{\Delta x}{\Delta t} = \frac{-15}{3} = -5$ [m/s]

(7)

となります。定義した速度ベクトルの方向は右向きで、その求まった符号が「－」ですからつまり方向が逆だったということになります。しかし答えは当然式(7)のように[m/s]です。出題者が軸神を設定しているからです。

忘れないうちに次の問題を解いてみましょう。

問3　速度を求めよ。

**図 9:** 速度を求めよ

車は左から右へと移動しています。では速度はどうなるでしょうか？…図10に軸神と速度ベクトルを書き込んでみましょう。

**図 10:** 軸神と速度矢印付加

ちゃんとこのように書き込めましたか？書き込めなかった人はまだ軸を確認する癖が付いてません。そしてその癖がついてないことは物理を学ぶ上で致命的な欠点になります。ちゃんとここで覚えてください。軸神が「左向きが正じゃ！」とか言っているので、これから求める「未知数」である速度ベクトルは当然軸神の設定に従います。そこで左向きになりますね。

では、速度を求めてみましょう。時間変化 $\Delta t$ は $\Delta t = 3 - 0$ [s]です。そして変位 $\Delta x$ は $\Delta x = 0 - 15$ [m]です。ですから求める速度は

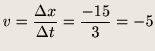$\displaystyle v = \frac{\Delta x}{\Delta t} = \frac{-15}{3} = -5$ [m/s]

(8)

となります。物体（車）の移動は図5と全く一緒です。しかし、求まった速度は式(6)とちょうど正負が反対の[m/s]になってしまいました。これは軸神が左が正と言っているからなのです。ですから、その正で速度ベクトルが左向きになりましたね。その左向きにおいて符号が「－」なので、つまり本当は右向きということです。しかし当然解答に書くべき答えは、軸神が正を決めてますから式(8)のように[m/s]となります。

ここで、疑問に思った方がいらっしゃるでしょうか？何故図5と図9は同じ運動をしているのに、軸の方向が変わっただけで速度の正負がかわったのだろうと…。

細かいところに注目した人は気付いたかも知れませんが、実は軸神が設定するのは正の方向だけではなく、軸の値全体なんですね。ですから、図5の場合は軸が右を向いていますから、その軸に付属する値（0や15）も右方向が大きくなりますね。しかし、図9においては、軸が左を向いていますから、当然その軸に付属する値も左方向へ大きくなるのです。

つまり軸の矢印の方向というのは正の方向を決めるだけでなく、その軸に付属する数字の増加方向も示すということのです。これが原因で、軸の方向が変わると速度の正負が変わってしまうのです。

では最後にもう一問だけやってみましょう。

問4　速度を求めよ。

**図 11:** 速度を求めよ

これは図7と同じように車は右から左へと移動しています。では速度はどうなるでしょうか？

**図 12:** 軸神と速度矢印付加

当然軸神が「左が正じゃ！」と言っているので、左が正ですよね。ですから「未知数」である求める速度ベクトルも当然左向きに設定します。

あとはいつもと同じように変化量を求めて…

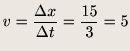$\displaystyle v = \frac{\Delta x}{\Delta t}= \frac{15}{3}= 5$ [m/s]

(9)

となります。式(9)の速度の符号は正になっていますので、書き込んだ図の速度ベクトル方向へ5[m/s]で移動するということですね。

さてここまで解っていただけたでしょうか？解らなかったらもう一度最初から問題を解きなおしてみて下さい。きっと最初に見たときと違った感覚で問題を解くことが出来ますよ。それは軸やベクトルの感覚が身に付いたサインです。物理が好きになる扉を一つ開けましたね。

次は加速度とは何かを説明いたします。

△上へ戻る

トップページへ | 物理トップページへ | アーカイブス | 次へ：速さとは | 戻る：力学とは

速度の定義 | 具体例 | 重要なお話 | 軸神登場 | ベクトル量の未知数 | まとめ | 例題

ホーム＞物理のトップページ＞目次＞力学とは＞速度とは