力学

バネが発揮する力

まずはバネが発揮する力です。経験的に何となく分かるんですよね、この力は。しかし当然そんなfeelingで乗り切ってもらっては困ります。それは問題が解けなくなるからです。やはりこのバネが発揮する力にも軸の概念は付きまといます。軸の概念が必要ないのは「力の大きさ」を聞かれたときだけです。ですからしっかりと理解しておきましょう。しかしまずはイメージから…。

△上へ戻る

力の大きさ

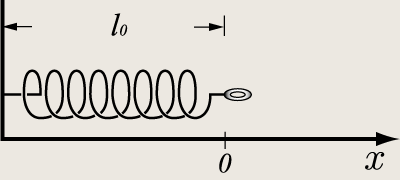**図 1:** 自然長のバネ「糸が発揮する力」に戻りますか？

図1は何も力を加えない状態のバネです。このときのバネの長さを「自然長」と呼びます。何も力を加えない自然なときの長さのことですね。

このバネを引いてもらいましょう！

**図 2:**バネを引く

ちょっと伸びましたね。図2の状態のバネの伸びを[m]と言います。決して[m]でないことに注意してください。この状態のとき、一体バネはどのような力を出しているのでしょうか？今回はバネが受けている力ではないですよ？バネが出している力を探してみましょう！

**図 3:**バネが出す力

もとの自然長からちょっとだけ引いたら、バネからちょっとだけ戻る方向に力が働きそうですね。思いっきり引っ張ったら、バネからとても大きな戻ろうとする力を受けるだろうという感覚はきっとあると思います。それを実験し式にしますと何とバネは自分の自然長からの伸び[m]に比例した力

$\displaystyle F = kx$

(1)式(3)に戻る

を、両端から内側向きに発揮するということがわかるわけです。もちろんこれはバネが発揮している力です。当然バネ自身には見えません。図3の向かって右側の[N]は少女にしか見えませんし、左側の[N]は壁にしか見えません。ここでは長さで表しています。

力が見えない方はきっと「つり合いの力」と「作用・反作用の関係」が理解できていません。
すぐ下のリンクをたどってください。

今[N]と言っている力は方向を気にせず大きさのみで取り扱っています。もう少し後で方向まで気にした定義の仕方に変えますので、今は大きさのみのイメージを頭に焼き付けてください。

△上へ戻る

バネを押す

今度はバネを押してみましょう。図4における少年はバネを軸負方向へ押しています。その結果バネは自然長から距離[m]だけ縮んでいます。したがって、この状態をバネの縮みが[m]であると表します。つり合いと作用・反作用に飛びますか？

**図 4:**バネを押して縮める

さて、バネは縮むと伸びる方向へ力を発生させます。つまり図5のようになります。

**図 5:**バネが出す力

この場合も、バネが伸びたときと同じようにバネが発する（少年を押す）力の大きさは

$\displaystyle F = kx$

(2)

となります。このはここでは長さで表しています。当然今回の力もバネには見えません。自分が出す力ですからね。この力が見えるのは少年と壁になります。

まとめますと、

バネは自然長に戻るように力を発揮し（復元力）、その力の大きさはkx [N]

となります。

△上へ戻る

方向を意識する

では今度は力の大きさではなく、ベクトル量として方向も意識しながら、バネがバネを引いたり押したりする物体（図では兄妹）にどのような力を与えるのかを考えてみましょう。壁にかかる力は考えませんので注意してください

まずは引くパターンからです。少女から引かれてしまうと、バネは距離[m]だけ伸びてしまいます。当然バネの自然長の位置を[m]とすると現在のバネの先端の位置は[m]となります。

**図 6:** バネを引く

そうすると、少女には次のような力がかかります。

$\displaystyle F=-kx$

(3)

まずはこのの表す意味が、式(1)のとは全く違うことを意識してください。式(1)のは、どれだけ伸びたかという長さを表します。それに対して、式(3)のは、軸に書いてある位置を表します。同じですが、長さ（スカラー量）として見るか、原点からの位置（ベクトル量）として見るかによって全く意味が異なりますので、注意が必要です。

式(3)の右辺は定数（スカラー量）のバネ定数とベクトル量であるの積で表されています。スカラー量はその場で何倍かという意味合いを持ちますので、結局ベクトル量が存在している以上、それらの積は方向と大きさの2つの値を持ちます。右辺がそのようなベクトル量を表すので、当然左辺もベクトル量になります。つまり、「右辺がベクトルを表すなら、当然左辺もベクトル量となる」というとてもイメージしやすい当たり前のことですね。

**図 7:** 式の意味

ところで、式(3)のはもちろん大丈夫ですよね。軸は向かって右方向へ向いてます。しかし少女に働くバネによる力は左方向（軸負方向）を向いていますので、式(3)のように「軸と逆方向だよ！」という意味で「」を付けるのです。

△上へ戻る

バネを押す場合

バネを押し込む少年の場合はどうでしょう？

**図 8:** バネを押す

バネは押されると元に戻りたがって少年を軸方向へ押します。ですから

$\displaystyle F=-kx$

(4)

となります。…!!?…アレ？間違ってまた「」を付けてるよ？と思った方がいらっしゃいますか？…まぁ確かに最初はそう思いますね。しかし、よく見てみてください。軸の原点はどこに設定してあるでしょうか？

**図 9:** 軸の0に注目

バネの自然長のところですよね。ということは今回は押し縮められていますので、の値は負（例えば[m]）になります。ですからそのまま

$\displaystyle F = kx$

(5)

としてしまうと、が負（[m]）ですからが負（[N]）となってしまいます。そうするともちろん軸向きが正ですから、少年にかかるバネからの力は軸の負方向に向いていることになってしまいます。明らかに変ですね。

ですから、が負となってもとしておけば全体で正となりますから、これで実際に私達がイメージするバネの力の方向と一致しました。結局バネは伸びようとも縮もうとも

$\displaystyle F=-kx$

(6)

と表されるわけです。これはバネが出す力の式(6)中のが軸上の点（基準点0からみた軸方向を正とするベクトル量）を表すことに起因します。しっかりと意識してください。

△上へ戻る

トップページへ | 物理トップページへ | アーカイブス | 次へ：バネの伸縮 | 戻る：力の種類

バネの力 | 力の大きさ | バネを押す場合 | 方向を意識する | バネを押す場合

ホーム＞物理のトップページ＞目次＞力学とは＞力の種類＞バネが発揮する力